
こんにちは!しょです!今日も元気です!
今日は習い事中に思い出した「人間の感覚は対数らしい」というのを書いていきたいと思います!
(ぼくは情報系の大学に行っていたのですが、そこで聞いた内容です。電磁系の授業なので、永遠にオイラーの定理に入れて数式を計算してくみたいな授業だったので、ぼくは

無理や~
とか思いながら単位は取れたのか取れなかったのかも思い出せません。 みなさんは10年も前に卒業した単位のことなんか覚えてますか?覚えてませんよね。そういうことです。まあそんなことはいいとして ※このカッコ内は読まなくていいです。たびたび出てきます)
結論
小さい値のほうが増分が大きい
→実生活にとっても合った増え方
本編
例えば1~10があったとして、例えば「1」と「2」のあいだって「1」ですよね??
それが、常用対数、つまり、底が10の時、
(常用対数か、自然対数かどっちかわからんくてウィキりました。(引用:https://ja.wikipedia.org/wiki/%E5%B8%B8%E7%94%A8%E5%AF%BE%E6%95%B0) 「本当に情報系の大学出てるんですか?プンスカ」 とか言ってくる人はよほどすごい学歴をお持ちだと思いますし、崇拝させていただきますので大学名をご記入いただければと思います。 どっちがどっちかなんて覚えていなくても「2つくらいあるらしいし、頑張れば底なんてなんでもいい」って覚えてるくらいで丁度いいんですよ。 99%の人(9千万人)は知らないんですから。 ただでさえ32歳のおっさんは74万人程度いるらしい(引用:https://www.stat.go.jp/naruhodo/c1data/02_05_stt.html)のですが、多分7千人ぐらい(1%)しか興味ないと思います。というか7千人も対数に興味ある方がやばいとさえ思う。 ※ここのカッコ内は読まなくていいです)
常用対数「log10◯≒?」の表
log1=0
log2≒0.3
log3≒0.5
log4≒0.6
log5≒0.7
log6≒0.8
log7≒0.8
log8≒0.9
log9≒1
log10≒1
(※小数点第2位を四捨五入してお送り致しております。)
「1.2.3.4.5.6.7.8.9.10」
と1づつ大きくなっていたとしたら、それが「人間の感覚」でいうと、
「0.3.5.6.7.8.8.9.10.10」
(※もとの値の10倍でお送りしてます。その方が小数点がなくわかりやすいので)
みたいな感覚で動いてるように「感じる」
整理すると、
| 自然数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 対数 | 0 | 3 | 5 | 6 | 7 | 8 | 8 | 9 | 10 | 10 |
グラフにするともっとわかりやすいかなっと思って作ってみました!
(※グラフは3回作り直しました!)
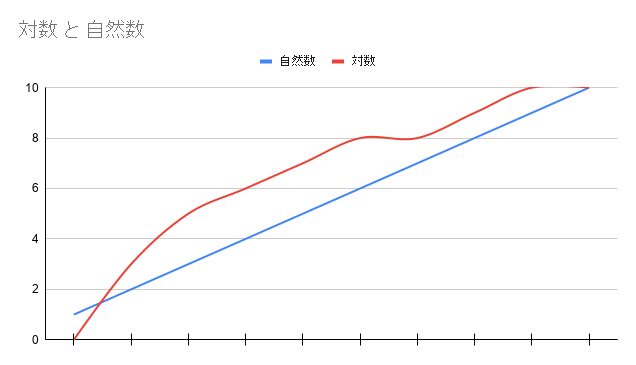
うーんなんかいまいちよくわかんないような気がするけど、(あ、というか、これの対数は四捨五入してしまった値なので、階段状になってしまってるけど、実際は2次関数を寝かしつけた感じになる。※読まなくても大丈夫です)見て欲しいところは、
「全体」
スッと先に立ち上がってる印象みたいなところ
自然数が「1」の時「0」だったのに、
自然数が「2」の時にすでに対数は「3」ですみたいな感じ。
「そんな勢いで立ち上がっちゃって大丈夫??」
って心配の声が上がりそうな感じ。
でも「少ない値の時にたくさん感じれる感覚器官」であったほうが動物が生存しやすそうな感じしませんか?
「小さな音でもよく聞こえる」
「暗くても少ない明かりで見える」
「少ない香りでも感じ取れる」
ほら。すごい生き延びれそう。
ここで増分も考えてみましょう。
どれくらい増えていってるかな~って感じのことです。
| 自然数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 対数 | 0 | 3 | 5 | 6 | 7 | 8 | 8 | 9 | 10 | 10 |
| 増分 | ー | 3 | 2 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
注目してほしいのは、
自然数が、「2」「3」の時、それぞれ3、2、とかなり大きな上げ幅です。
しかし、「4」からは、1より上はもう増えません。
つまり自然数で「3」の時、もう「半分くらいな感覚」
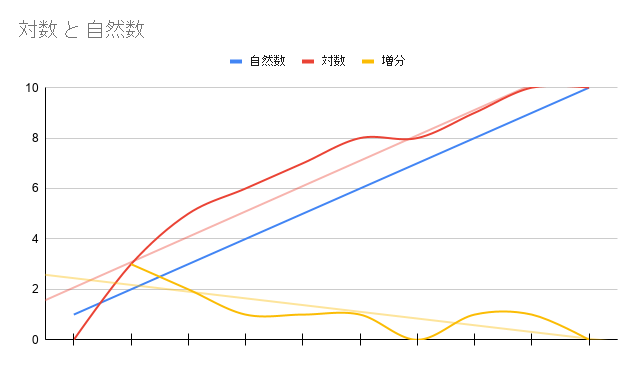
グラフも作っちゃいました。
重ね合わせただけですけどね。
「googleスプレッドシート」に「トレンドライン」という機能があったので、黄色い線が引っ張ってあると思いますが、どんどん下がっていってるっていうのが分かりやすくなりましたね。
先程の自然数「3」の時、感覚で「半分くらい」っていうのは実生活で大きく使われています。
例えば
「トップ3」
→3ぐらいまで押さえとけば半分くらい押さえたようなもの
「シェア3割」
→3割押さえてたらだいぶすごい企業
自然数で「6」になったらもう感覚で「8割」です。
自然数の「+1感覚」と、
人間が感じる「+1感覚」
ちょっとずれているっていうのが感じ取っていただけましたか?
まとめ
「小さい値のほうが増え方が大きい」
→その増え方である「対数」は実生活に合っている
というのを実感していただきたかったのですが、いかがでしたでしょうか。
音とかで使われる「デシベル(dB)」というのも実は対数なんですよ!
長々とした文章を書く前から普段から使っていたという。
デシベル自体は「デシ」部分と「ベル」部分に分かれています。
「デシ(d)」・・・デシリットル(dL)とかの「デシ」10分の1という意味です。
こういうのを「接頭辞」とか言います
「ベル(B)」・・・簡単に言うとゼロの数。「2ベル」=100、5B=100000
ついでに地震でおなじみの「マグニチュード」も増え方は対数なので大きな値になるほど増え方は小さくなります。
値が増えていくと増え方が小さくなる。
対数の特性をうまく利用しています。
ぼくは対数についてそんなによく知りませんが、なんとなく好きです。
なんか高機能だから。
皆さんにもそんな気持ちで対数に接していただけたら幸いです。
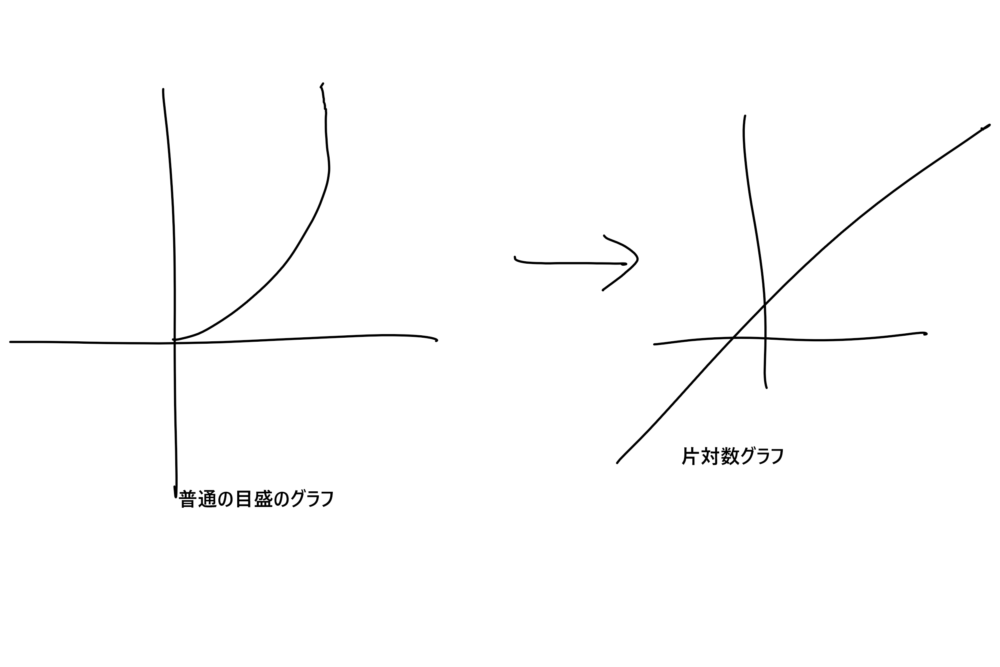
片対数グラフにすると直線になってくれるところがかわいいです。
最後に

読んでいただいてありがとうございました!
嬉しくて泣いた
もっと読みたいなと思ったらツイッターで「読みたいな」って言ってただけたら張り切ってもっと書いちゃいます!
他の記事も読んでみてくださいね!
よろしくおねがいします。

コメント